খরগোসের অঙ্কের গল্প

অভিজিৎ কর গুপ্ত

একটা সাধারণ অঙ্কের বই। তাতে আছে পাটিগণিতের নানান অঙ্ক। এর মধ্যে একটা অঙ্ক আছে খরগোস নিয়ে।

একজোড়া খরগোস – একটা মেয়ে খরগোস, আর একটা ছেলে। এক মাস পর পরিণত হলে তারা মিলিত হয় এবং তার একমাস পর এরকমই আরেক জোড়া খরগোসের বাচ্চা দেয়। আবার এই বাচ্চাগুলোও এভাবেই একমাস পর পরিণত হয়ে আরো একমাস পর তেমনই এক জোড়া খরগোসের বাচ্চা দেয় (ধরে নিতে হবে, একবার পরিণত হয়ে গেলে এক এক জোড়া খরগোস প্রতি মাসে এক জোড়া করে বাচ্চা দিতে থাকে। কোনো খরগোসের মৃত্যু নেই।)। এই নিয়মে এক বছরের শেষে কতজোড়া খরগোস থাকবে?

ধাপে ধাপে হিসাব করে এগোলে অঙ্কটা সহজেই করে ফেলা যায়। ধরা যাক, শুরুতে একজোড়া খরগোস। তাহলে একমাস পর ওই একজোড়া খরগোস পরিণত হবে। সুতরাং তখনো একজোড়া খরগোসই থাকবে। দ্বিতীয় মাসে এদের থেকে একজোড়া খরগোস বাচ্চা জন্মাবে। তাহলে এখন, নতুন আর পুরোনো মিলিয়ে 1 + 1 = 2, অর্থাৎ দুজোড়া খরগোস থাকবে। এরপর তৃতীয় মাসের শেষে পুরোনো জোড়া খরগোস থেকে আরো একজোড়া খরগোস-এর বাচ্চা হবে, আর ইতিমধ্যে আগের একজোড়া বাচ্চা এখন পরিণত হবে। তাহলে, নতুন পুরোনো মিলিয়ে এখন মোট 2 + 1 = 3 জোড়া খরগোস থাকবে। এর পরের মাসের শেষে পরিণত দুজোড়া খরগোস আরো দুজোড়া বাচ্চা দেবে আর সেসময় আগের মাসে জন্মানো একজোড়া খরগোস পরিণত হবে। তাহলে, এবার সব মিলিয়ে 3 + 2 = 5 জোড়া খরগোস থাকবে। এইরকম নিয়মে চলতে থাকলে পরপর মাসগুলোর শেষে যত জোড়া খরগোস থাকবে সেই সংখ্যাগুলোকে পাশাপাশি লিখলে হবে, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…এইরকম সব সংখ্যার একটা সিরিজ। একে বলে ফিবোনাচি সিরিজ (Fibonacci Series)। এরকম একটা নাম কেন আর কেনই বা এর গুরুত্ব সেটা পরে বলছি।

পাটিগণিতের যে বইতে এই খরগোসের অঙ্কটা করতে দেওয়া ছিলো তার নাম লিবার আবাচি (Liber abbaci, লাইবার আব্বাচি), ইতালিয়ান ভাষায় লেখা একটা বই। প্রথম প্রকাশ ১২০২ সালে। ল্যাটিন ও ইতালিয়ান ভাষায় abbaci হলো abbacus অর্থাৎ গণনা। তবে, আমরা যে abbacus যন্ত্রের সাথে এখন পরিচিত, সেটা পরে এসেছিলো চীন দেশ থেকে। অবশ্য ইউরোপ এবং পৃথবীর বহু জায়গায় গণনা করার জন্য একসময় নানা ধরণের অ্যাবাকাস যন্ত্রের চল ছিলো। Liber abbaci হলো Book of calculation! বইয়ের লেখকের পুরো নাম সঠিকভাবে কেউ জানে না। ভিতরের পাতায় পরিচয়পত্র বা মুখবন্ধ থেকে জানা যায় তাঁর নাম Leonardo Pisano (Leonardo of Pisa) বা পিসার লিওনার্দো। ইউরোপের অনেক জায়গায় তখন অনেকসময় এরকমই লেখা হত। যেমন, লিওনার্দোর সমসাময়িক একজন ইঞ্জিনিয়ার, Bonnano Pisano (পিসা শহরের Bonnano) যিনি পিসার বিখ্যাত ঘণ্টা টাওয়ার নির্মাণের তদারক করছিলেন।

ইতালির পিসা শহরের কথা কেই বা না জানে। আর, সেখানকার অত্যাশ্চর্য সেই ঘণ্টা টাওয়ার বা হেলানো টাওয়ার-এর কথা নিশ্চয়ই পড়েছো ইস্কুলের বইতে। সেই যে, হেলানো টাওয়ার থেকে গ্যালিলিওর গিনি ও পালকের পরীক্ষা! মনে হয় এরকম একটা জায়গা থেকেই তো পদার্থবিদ্যার শুরু। অপূর্ব সুন্দর এই পিসা শহর, একসময় ছিলো ভূমধ্যসাগরের ধারে জমজমাট এক বন্দর। এর কাছেই আরেকটা অসাধারণ সুন্দর শহর ফ্লোরেন্স। ইতালিতে এসে পৌঁছালে রোম, ফ্লোরেন্স, পিসা, ভেনিস, মিলান, জেনোয়া, পাদোয়া এসব পুরোনো শহর ঘুরে দেখতেই হয়! প্রত্যেক শহরই বহন করছে অপূর্ব সব ভাস্কর্য, চিত্রকলা আর অঙ্ক, বিজ্ঞান চর্চার সাক্ষ্য! ঘুরতে ঘুরতে পিসা শহরে এসে পড়লে, Campo dei Miracoli বা Square of Miracles চত্বরে সেই হেলানো টাওয়ার বা ক্যাথিড্রালের ঘন্টা টাওয়ারের সামনে এসে থমকে যেতে হয় বৈকি! আবেগে তখন আপ্লুত হয়ে ওঠে মন।

১১৮৫ সালে বাবার নির্দেশে বছর পনেরোর লিওনার্দো জাহাজে চড়ে ভূমধ্যসাগর পেরিয়ে এসে পড়েছিলো আরব দুনিয়ায়। সেখানে পরম বিস্ময়ের সাথে সে দেখতে থাকে সবকিছু। উত্তর আফ্রিকায় এখনকার আলজেরিয়া দেশের বন্দর শহর বুগিয়া (Bugia, এখনকার নাম বেইজিয়া, Béjaïa)। লিওনার্দোর বাবা আগেই এখানে ব্যাবসাবাণিজ্য বা কমার্সের কাজ নিয়ে চলে এসেছিলেন পিসার বড় বড় মার্চেন্টদের প্রতিনিধি হিসাবে কাস্টমস অফিসার-এর কাজ নিয়ে। বুগিয়ার বাজার এলাকার সাধারণ মানুষজন আর ব্যবসায়ী লোকজনদের কথাবার্তা, তাদের লেনদেনের হিসাবনিকাশ-এর পদ্ধতি এসবকিছুই অত্যন্ত আগ্রহ নিয়ে ঘুরে ঘুরে দেখতে থাকে লিওনার্দো। স্থানীয় লাইব্রেরিতে যায় সে, অনেক অঙ্কের বই উল্টেপাল্টে দেখে বুঝতে পারে সেখানকার দুনিয়ায় অঙ্কের হিসাব নিকাশ একেবারে অন্যরকম। ইন্দো-আরবীয় পদ্ধতি বা ডেসিমাল সিস্টেমে অঙ্কের হিসাব করার যে সুবিধা তা সে বুঝে যায় একটু একটু করে। দশমিক পদ্ধতি বা ডেসিমাল সিস্টেমে 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 এই দশটা ডিজিট দিয়ে কি করে বড় বড় সংখ্যা তৈরি করা যাচ্ছে আর অনায়াসে গুণ ভাগ করে ফেলা হচ্ছে, এসব দেখে লিওনার্দো একেবারে হতবাক।

ত্রয়োদশ শতকের প্রথমদিক পর্যন্ত ইউরোপে তখনো রোমান সিস্টেমে অঙ্ক করা হতো। প্রধানত ব্যবসা বা কমার্সের কাজ। সাধারণ মানুষের পক্ষে সেসব বোঝা বেশ মুশকিল ছিল। অবশ্য সেখানকার কিছু গণিতজ্ঞ ও পন্ডিত মানুষেরা ইন্দো-আরবীয় পদ্ধতিতে অঙ্ক করার কথা জানতেন। তবে তা যে কখনো ব্যাবসার হিসাব অথবা দৈনন্দিন জীবনের কাজে আসবে কিংবা এই পদ্ধতি কাজে লাগিয়ে আরো কিছু ভাবনা চিন্তা করা যাবে এবিষয়ে তাঁদের কোনো মাথা ব্যাথা ছিল না। তাঁদের কাছে এটা ছিলো নিছকই হিসাব করার আরেকটা পদ্ধতি।

রোমান সংখ্যার (Roman numerals) বিষয়ে আমরা সবাই অল্পবিস্তর জানি। আমাদের সভ্যতা সংস্কৃতিতে এখনো এর চল আছে। ধরো, তুমি ক্লাস সেভেন বা ক্লাস ইলেভেন-এ পড়ছো। তাহলে VII বা XI লেখা হবে। আবার, পুরোনো যুগের অনেক স্থাপত্যের গায়ে খোদাই করা রোমান সংখ্যা বা ডিজিটগুলো দেখতে পাবে। অনেক বড় বড় ঘড়িতেও এখনো অনেকসময় রোমান ডিজিট দিয়ে লেখা হয়। তবে, অঙ্ক করা বা হিসাবনিকাশের জন্য আমরা কখনো তা ব্যবহার করি না। রোমান সিস্টেমে পরপর দাগ কেটে I, II, III লেখা হয় 1, 2, 3 বোঝানোর জন্য। আবার 5 বোঝাতে লেখা হয় V চিহ্ণ। এর আগের সংখ্যা 4 বোঝাবার জন্য চারটে দাগ না টেনে, 4 = 5 – 1 অর্থাৎ V – I বোঝাতে IV লেখা হয়। তারপর দ্যাখো, পরের সংখ্যাগুলোর জন্য VI, VII, VIII এরকম ভাবে 8 অবধি লেখা হচ্ছে। এরপর 10 বোঝাবার জন্য আরেকটা চিহ্ণ X লেখা হলো। সুতরাং, দশের আগের সংখ্যা বোঝাতে 9 = 10 – 1 অর্থাৎ X – I কে IX লেখা হচ্ছে। ধরা যাক, 39 লিখতে চাই, তাহলে ভাবতে হবে, 39 = 10 + 10 + 10 + 9, অর্থাৎ XXXIX লিখতে হবে। আরো বড় সংখ্যা, যেমন 50, 100, 500, 1000 লেখার জন্য ব্যবহার করা হচ্ছে যথাক্রমে L, C, D, M এই চিহ্ণগুলো। এবার একই কায়দায় 40 = 50 – 10 ভেবে L – X বোঝাতে গিয়ে XL লেখা হলো। এবার তাহলে, 49 = 40 + 9 বোঝানোর জন্য XLIX লিখতে হবে। ধরা যাক, লিখতে চাইছো 2022 সাল, তাহলে ভাবতে হবে 2022 = 1000 + 1000 + 10 + 10 + 2, তার মানে MMXXII লিখতে হবে। কাজেই বোঝা যাচ্ছে, বড় বড় সংখ্যাগুলো লিখতে গেলে বেশ খেয়াল রাখতে হচ্ছে, চিহ্ণগুলো পরপর জুড়ে লম্বা করা হচ্ছে, আবার নতুন নতুন চিহ্ণ ব্যবহার করতে হচ্ছে। এরকম রোমান সংখ্যা দিয়ে যোগ বিয়োগ করাটাও বেশ ঝামেলার। মনে করা যাক, খুব সাধারণ একটা যোগ, 34 + 20 = 54 করতে চাইছো। তাহলে, XXXIV + XX লিখে গুনে দেখতে হবে একই চিহ্ণ কতগুলো আছে, যেমন এখান ৫ টা X আছে, তাই যোগ করার সময় X + X + X + X + X = L লিখলে, যোগফল LIV হবে। এভাবে বড় বড় যোগ করার সময় কত কি সব মাথায় রাখতে হবে। বিয়োগ করার কাজটাও করা যাবে এরকম সব খেয়াল রেখে। তবে গুণ বা ভাগের অঙ্ক করতে গেলে মুশকিল। তাই যোগ বা বিয়োগ করে করেই এগোতে হবে। কাজেই বোঝা যাচ্ছে, ইউরোপের সাধারণ মানুষ-এর কাছে সেসময় অঙ্কের সাধারণ হিসাবনিকাশও ছিল বেশ জটিল ব্যাপার।

লিওনার্দো দেখলো, ইন্দো-আরবীয় পদ্ধতিতে বা ডেসিমাল সিস্টেমে দশটা ডিজিট কে পাশাপাশি বিভিন্ন ঘরে বা কলামে টেবিল আকারে সাজিয়ে ইচ্ছামতো ছোটো বড় যেমন খুশি সংখ্যা তৈরি করা যাচ্ছে। এতে অঙ্কের হিসাব করা যাচ্ছে অনেক সহজে। ডিজিটগুলো বিভিন্ন ঘরে বসিয়ে একক-দশক-শতক-হাজার…এভাবে সংখ্যা তৈরি করতে আমরা অভ্যস্ত। প্রাচীন ভারতবর্ষে এরকম গণনার পদ্ধতি চালু ছিল। অবশ্য আরো অনেক জায়গায় এরকম চেষ্টা হয়েছে। যেমন, মেসোপটেমিয়া ও ব্যাবিলনীয় সভ্যতায় (এখনকার ইরান, ইরাক, সিরিয়া ইত্যাদি নিয়ে যে অঞ্চল) ৬০ খানা ঘর (60 base system) ব্যবহার করা হতো। এর প্রভাবও আমাদের সভ্যতায় এখনো রয়ে গেছে। এই যে আমরা সময়ের হিসাব করার জন্য এক ঘণ্টা = ৬০ মিনিট, ১ মিনিট = ৬০ সেকেন্ড লিখি, আবার ১ ডিগ্রী মাপের কোণ কে ৬০ ভাগে ভাগ করে এক একটা ভাগকে ১ মিনিট বলি, তারপর ১ মিনিট কোণ কে আবার ৬০ ভাগে ভাগ করে এক সেকেন্ড কোণ বলি এসবই হচ্ছে তার প্রমাণ। তবে, প্রয়োজনমতো এক একটা ঘরে শূণ্য বসিয়ে সংখ্যাগুলোর গুরুত্ব বাড়ানো কমানো বা অঙ্কের হিসাবে তার থেকে যে সুবিধা পাওয়া এসব তারা ভাবতে পারে নি। প্রাচীন ভারতের বিখ্যাত জ্যোতির্বিদ ও গণিতজ্ঞ ব্রহ্মগুপ্ত (598 – 668 খ্রীষ্টাব্দ) প্রথম এই শূণ্যের ধারণা তৈরি করলেন। টেবিল আকারে ডিজিটগুলো বিভিন্ন ঘরে বসানোর পর ফাঁকা ঘর বা কলামগুলো চিহ্ণিত করার জন্য হয়ত প্রথমে গোল করে দাগ দেওয়া হয়েছিলো। তারপর সেখান থেকেই হয়ত শূণ্য চিহ্ণ-এর ভাবনাটা আসে।

প্রাচীন ভারতের এই উপমহাদেশের সাথে আরব দুনিয়ার দেশগুলোর নিয়মিত ব্যাবসাবাণিজ্যের যোগাযোগ ছিলো। ভারত ও শ্রীলঙ্কা থেকে মশলাপাতি, ওষুধ, গন্ধদ্রব্য, রং, সিল্ক ইত্যাদি সিল্ক রোড ধরে আরবের দেশগুলোতে যেত। তারপর এর সাথে সেখানকার দুধজাত জিনিস, ফল ইত্যাদি চলে যেত ভূমধ্যসাগর পেরিয়ে ইউরোপের দেশগুলোতে। আবার ওদিক থেকে আসত চামড়ার জিনিসপত্র, মোম ইত্যাদি। তথ্য ও সংস্কৃতির আদানপ্রদানও যে এভাবেই মূলতঃ বাণিজ্যের হাত ধরেই হয়েছে তা বোঝা যায়। এভাবেই একসময় ভারতবর্ষে চালু থাকা দশমিক পদ্ধতি আরব দুনিয়াতে গিয়ে পৌঁছায়। তারপর আরব পণ্ডিতদের হাতে পড়ে তা আরো পরিণত হয়, অঙ্কের নানা কিছু হিসাব করার পদ্ধতি আবিষ্কার হতে থাকে। জটিল সব পাটিগণিতের অঙ্ক প্রতীক চিহ্ণ ব্যবহার করে কিভাবে সহজে করা যায় তা আবিষ্কার হয় সেখানে। অর্থাৎ বীজগণিত তৈরি হয়।

আরব দুনিয়া থেকে একসময় দেশে ফিরে গিয়ে লিওনার্দো পিসানো তাঁর সমস্ত অভিজ্ঞতা ও জ্ঞান থেকে লিখে ফেললেন ৬০০ পাতার সেই অঙ্কের বই লিবার আবাচি (Liber abbaci)। মূলতঃ ব্যাবসা-বাণিজ্যের হিসাব নিকাশের অনেক সুবিধা হবে, এই ভেবেই লেখা। সাধারণ পাঠক যাতে পড়ে বুঝতে পারে তার জন্য ইন্দো-আরবীয় সিস্টেম, বীজগণিতের পদ্ধতির বর্ণনা এসব বিস্তারিত লিখলেন তিনি এই বইতে। আর, উদাহরণ হিসাবে, নতুন পদ্ধতি বোঝাতে জুড়লেন বাস্তব জীবনের অভিজ্ঞতা থেকে নেওয়া প্রচুর অঙ্ক। এসবের মধ্যেই ছিল খরগোসের ওই সাধারণ অঙ্ক যা থেকে তৈরি হলো ফিবোনাচি সিরিজ। অবশ্য গবেষণা থেকে দেখা গেছে ওই বইয়ের বেশীরভাগ অঙ্কই সংগ্রহ করা। যেমন, তথাকথিত এই ফিবোনাচি সিরিজের কথা জানা ছিল প্রাচীন ভারতে। তৃতীয় (বা দ্বিতীয়) খ্রীষ্টাপূর্ব সময়ে রাজস্থান অঞ্চলে সংস্কৃত পন্ডিত ও কবি পিঙ্গালা (Pingala)-এর লেখা বিখ্যাত ছন্দশাস্ত্র-এর বিশ্লেষণ থেকে দেখা যায় সেখানে ছন্দ ও মাত্রার ব্যবহার হচ্ছে এরকমই একটা অঙ্কের সিরিজ দিয়ে (ইংরেজিতে বলে prosody, the pattern of sound and rhythm in poetry)। অবশ্য তা নিয়ে অঙ্ক করার কথা কেউ ভাবেন নি তখন। দীর্ঘ সময় পেরিয়ে ষষ্ঠ শতকে কবি ও গণিতজ্ঞ বিরাহাঙ্কা (Virahanka) এই সিরিজ দিয়ে তৈরি করলেন ছন্দের কম্পোজিশন, দেখালেন কিভাবে ছোটো ও বড় সিলেবল জুড়ে এইরকম একটা সিরিজ দিয়ে অপূর্ব সুন্দর ছন্দের কম্পোজিশন করা যায়। আরো দীর্ঘকাল পেরিয়ে, ১১৫০ সালে জৈন দার্শনিক হেমচন্দ্র (Hemchandra) এই সিরিজ দিয়ে টেক্সট কম্পোজ করলেন। সুতরাং, তথাকথিত ওই ফিবোনাচি সিরিজ কে পিঙ্গালা সিরিজ বা বিরাহাঙ্কা সিরিজ অথবা হেমচন্দ্র সিরিজও অনেকে বলেন।

লিবার আবাচি বই যখন পিসাতে প্রকাশিত হলো, তখনও ছাপাখানা (printing press) আবিষ্কার হয় নি। তাই খুব যত্ন নিয়ে হাতেই লেখা হয়েছিল বেশ কয়েকটা কপি। বই প্রকাশের পর রাতারাতি হিরো হয়ে উঠলেন লিওনার্দো। পিসার সীমানা ছাড়িয়ে, ফ্লোরেন্স ভেনিস হয়ে গোটা ইউরোপে ছড়িয়ে পড়লো তাঁর খ্যাতি। হোলি রোমান সম্রাট দ্বিতীয় ফ্রেড্রিকও লিওনার্দোর বক্তব্য ও আরব দুনিয়ার আশ্চর্য অঙ্কের পদ্ধতির কথা শুনতে আগ্রহ প্রকাশ করলেন।

লিওনার্দোর সময়ের পর, পরবর্তী তিনশো বছর ধরে সারা ইউরোপে হাজার হাজার অঙ্কের বই প্রকাশিত হয়েছে এই ইন্দো-আরবীয় পদ্ধতির উপর। তবে, লিওনার্দোর কথা কেউ আর বিশেষ মনে রাখে নি। সেসময়ে আগের লেখক বা স্কলারদের নাম উল্লেখ করা বা লিখিত ক্রেডিট দেওয়ার খুব একটা চল ছিল না। লিবার অ্যাবাচির বেশ কয়েকটা হাতে লেখা কপির মধ্যে তিনটে মাত্র কপি বেঁচে আছে। রোম, ফ্লোরেন্স আর জেনোয়ার মিউজিয়ামে আছে সেগুলো। পনেরোশো শতকের মাঝামাঝি ইতালীয়ান লুকা প্যাচিওলি (Luca Pacioli) একটা অঙ্কের বই (On Arithmetic, Geometry, Proportion and Proportionality) লেখেন। এই বইয়ের কোনো এক পাতায় তিনি লিওনার্দো পিসানোর কথা উল্লেখ করেন। ব্যাস এটুকুই। এর পর কেটে গেছে আরো কয়েকটা শতক। লিওনার্দো পিসানো প্রায় বিস্মৃতির অন্তরালেই থেকে গেছেন। পিয়েত্রো কোসালি (Pietro Cossali) ১৭৯৭ এবং ১৭৯৯ সালে দুটো ভল্যুম-এর বই, ‘History of Professsional Mathematics’ লিখতে গিয়ে বিস্তর গবেষণা করে বার করেন Leonardo Pisano-এর অবদানের কথা।

Liber abbaci বইয়ের মুখবন্ধে লিওনার্দো লিখেছিলেন filius Bonacci অর্থাৎ তিনি Bonacci পরিবারের ছেলে। এই শব্দবন্ধ থেকেই ১৮৭০ সালে ফরাসী গণিতজ্ঞ এদুয়ার্দ লুকা (Edouard Lucas) লেখকের নাম Fibonacci লিখে দেন। তারপর থেকেই এই ‘ফিবোনাচি’ নাম টা রয়ে গেছে। Fibonacci-এর Liber abbaci বইয়ের দ্বিতীয় সংস্করণ বেরিয়েছিল বেশ কয়েক বছর পরে। তারপর আরো কয়েকটা অঙ্কের বইও লেখেন তিনি। কিন্তু, সেসব আর কেউ মনে রাখে নি। এমনকি লিবার অ্যাবাচি বইয়ের অজস্র বাস্তবধর্মী অঙ্কের কথাও আর কারো মনে নেই। শুধু সেই খরগোসের অঙ্কের নাম্বার সিরিজটা আশ্চর্যভাবে বহু শতাব্দী পেরিয়ে আজও Fibonacci series হিসাবে হয়ে রয়ে গেছে আমাদের সভ্যতা ও সংস্কৃতিতে।

একটু খেয়াল করে দেখা যাবে, ফিবোনাচি সিরিজে (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,…)-এর যে কোনো পর পর দুটো সংখ্যা যোগ করলে তার ঠিক পরের সংখ্যাটা পাওয়া যায়। যেমন, 2 + 3 = 5, 5 + 8 = 13, 8 + 13 = 21,…ইত্যাদি। একটা মজার ব্যাপার হলো, এই সিরিজের একটা সংখ্যার সাথে তার ঠিক আগের সংখ্যার অনুপাত, ক্রমান্বয়ে যত সিরিজ এগোতে থাকবে, একটা নির্দিষ্ট ভগ্নাংশ সংখ্যা (1.618…)-এর দিকে যাবে। যেমন, 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.6153846…, 377/233 = 1.6180257, 987/610 = 1.6180327… এইরকম ব্যাপার। এই অনুপাত (1.618…) কে বলা হয় গোল্ডেন রেসিও (Golden ratio)!

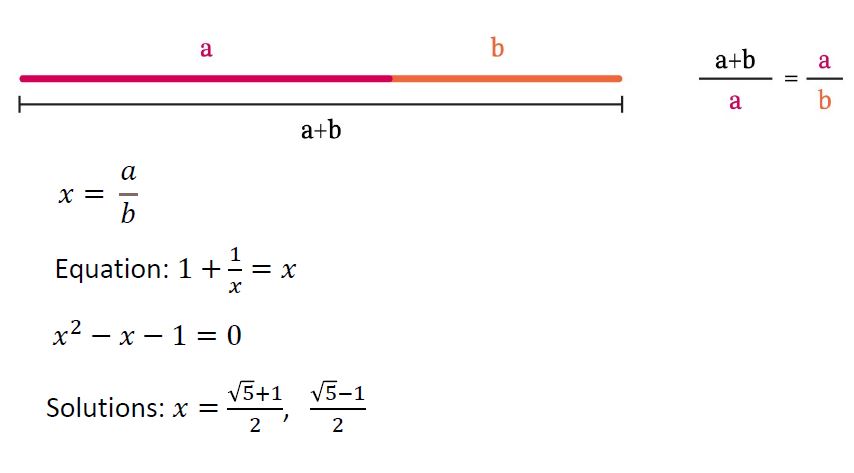
একটা হিসাব করা যাক। ফিবোনাচি সিরিজের বহু দূরবর্তী পরপর তিনটে সংখ্যাকে a, b, a+b ধরা যাক। তাহলে আমরা লিখতে পারি (যেহেতু অনুপাত একই সংখ্যার দিকে এগোয়),

(a + b)/b = b/a

a/b + 1 = b/a

এবার যদি b/a = x লিখি, তাহলে

1/x + 1 = x

অতএব,

x^2 – x – 1 = 0

তাহলে, আমরা অতি পরিচিত একটা দ্বিঘাত সমীকরণ পেলাম। স্কুলের অঙ্কের বইতে এরকম দ্বিঘাত সমীকরণ সমাধানের জন্য আমরা প্রাচীন ভারতীয় গণিতজ্ঞ শ্রীধর আচার্য (Sreedhara Acharya)-এর ফর্মূলা ব্যবহার করেছি। তাহলে, এখানে দুটো সমাধান হবে

(√5 + 1)/2 = 1.618… এবং (√5 – 1)/2 = 0.618…

চিত্র ২: ফিবোনাচি সিরিজের সংখ্যাগুলোকে এক একটা বর্গক্ষেত্রের বাহু ধরে নিয়ে এরকম বর্গক্ষেত্রগুলোকে ছোটো থেকে বড় পাশাপাশি মাপমতো বসিয়ে বর্গক্ষেত্রের এক কোনা থেকে উলটো দিকের কোনা পর্যন্ত ক্রমাগত বৃত্তচাপ দিয়ে জুড়তে থাকলে একটা স্পাইরাল তৈরি হচ্ছে। আরো অনেক মজার ব্যাপার আছে। যেমন, ফিবোনাচি সিরিজের সংখ্যাগুলোকে এক একটা বর্গক্ষেত্রের বাহু ধরে নিয়ে এরকম বর্গক্ষেত্রগুলোকে ছোটো থেকে বড় পাশাপাশি মাপমতো বসিয়ে তারপর এক একটা বর্গক্ষেত্রের এক কোনা থেকে উলটো দিকের কোনা পর্যন্ত ক্রমাগত বৃত্তচাপ দিয়ে জুড়তে থাকলে একটা স্পাইরাল তৈরি হবে (চিত্র – ২)। একে বলে গোল্ডেন স্পাইরাল (Golden spiral)!

ফিবোনাচি নাম্বার সিরিজ নিয়ে সাধারণ মানুষ থেকে সংখ্যাতত্ত্ববিদ পর্যন্ত সবারই উৎসাহ আর নিত্যনতুন বিশ্লেষণের অভাব নেই। খাতাকলম নিয়ে তোমরাও বসে যেতে পারো। নিজেরাই আবিষ্কার করতে পারো সংখ্যার সিরিজের সাথে জ্যামিতির ঘনিষ্ঠ সম্পর্ক। এই যেমন, ফিবোনাচি সিরিজের সংখ্যাগুলো কে বর্গ করলে, 1^2, 1^2, 2^2, 3^2, 5^2, 8^2… অর্থাৎ 1, 1, 4, 9, 25, 64,…এইরকম সিরিজ হবে। যেহেতু বর্গ করা হয়েছে, তাই ভাবা যেতে পারে, এরা এক একটা বর্গক্ষেত্রে ক্ষেত্রফল। আগেই বলেছি, গোল্ডেন স্পাইরাল তৈরি করার সময় ফিবোনাচি সিরিজের এক একট সংখ্যা কে বর্গক্ষেত্রের বাহু ধরে নিয়ে বর্গক্ষেত্রগুলো পাশাপাশি জায়গামতো বসালে আয়তক্ষেত্র হবে। তাহলে দেখো, এখন যদি এই বর্গ করা সিরিজের সংখ্যাগুলো পর পর যোগ করা যায়, তবে তা হবে এক একটা আয়তক্ষেত্রের ক্ষেত্রফল। তার মানে ধরো, 1 + 1 + 4 = 6 = 2 x 3, অর্থাৎ প্রথম তিনটে বর্গক্ষেত্র জুড়ে যে আয়তক্ষেত্র হলো তার ক্ষেত্রফল 6 একক এবং তার দুটো বাহুর দৈর্ঘ্য 2 এবং 3 একক। খেয়াল করে দেখো, এখানে 2 এবং 3, এরা কিন্তু, ফিবোনাচি নাম্বার। এভাবে আরো দেখতে থাকো, 1 + 1 + 4 + 9 = 15 = 3 x 5 (আবার দুটো ফিবোনাচি নাম্বার)! জ্যামিতিক ছবি এঁকে দেখলে বিষয়টা আরো স্পষ্ট হবে।

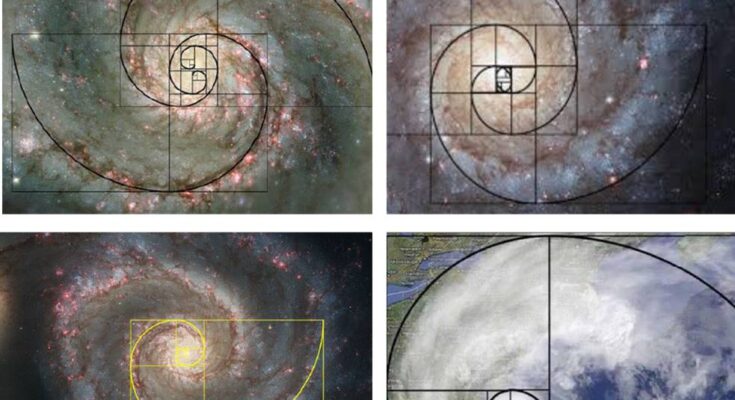
বিস্ময়ের ব্যাপার হলো, এই ফিবোনাচি নাম্বার, গোল্ডেন রেসিও, গোল্ডেন স্পাইরাল ঘুরে ফিরে বিভিন্ন জায়গায়, বিভিন্ন আলোচনায় এসে পড়ছে। প্রকৃতিতে নানা ধরণের ফুল পর্যবেক্ষণ করে দেখা যাচ্ছে, বহু ফুলেরই পাপড়ির সংখ্যা ফিবোনাচি নাম্বার দিয়ে আসছে। যেমন, এক পাপড়িওলা ফুল, তিনটে পাপড়িওলা ফুল, পাঁচটা আটটা,…একুশ, চৌত্রিশ এরকম সব সংখ্যার পাপড়িওলা ফুলের অসংখ্য উপস্থিতি দেখা যাচ্ছে প্রকৃতিতে। আবার, দেখা যাবে সূর্যমুখি ফুলের উপর বীজগুলো অদ্ভুতভাবে এদিক ওদিক স্পাইরাল প্যাটার্নে সাজানো থাকে। গুনে দেখা যায়, এক একটা স্পাইরাল বাহুর মধ্যে বীজের সংখ্যাও ফিবোনাচি নাম্বার দিয়ে আসছে। আরো বহু ক্ষেত্রে, যেমন পাইন কোনের উপর প্যাটার্ন, অনেক সামুদ্রিক শাঁখের উপর প্যাটার্ন (নটিলাসের ডিজাইন), কিছু ফার্ণ, বিশেষ ধরণের অ্যালোভেরা গাছের পাতার বিন্যাস, ব্রকোলি অথবা ধরো ক্যামেলিয়ন (গিরগিটি জাতীয়)-এর গোটানো ল্যাজ-এর বাহার এসব আরো সব কত কি, সবজায়গাতেই যেন এই গোল্ডেন স্পাইরাল বা ফিবোনাচি স্পাইরালের উপস্থিতি (চিত্র – ৪)। আবার স্যাটেলাইট ম্যাপে দেখা সাইক্লোনের প্যাটার্ন, মহাকাশে স্পাইরাল গ্যালাক্সি এসবের জ্যামিতিতেও গোল্ডেন স্পাইরালের আশ্চর্য উপস্থিতি! এর কি কোনো কারণ আছে? এ নিয়ে অনেক বিশ্লেষণ আছে, অনেক গবেষণা আছে। তবে প্রকৃতিতে এইরকম সংখ্যা ও জ্যামিতির উপস্থিতি হয়ত অজান্তেই আমাদের মনের মধ্যে একটা প্রভাব বিস্তার করেছে, আমাদের শিল্প সংস্কৃতিতে তার ছাপ পড়েছে একটা দৃষ্টিনন্দন ব্যাপার হিসাবে। লিওনার্দো দ্য ভিঞ্চির বিখ্যাত সব ছবি – মোনালিস (Mona Lisa), দ্য লাস্ট সাপার (The Last Supper), ভিত্রুভিয়ান ম্যান (Vitruvian Man)-এর মধ্যে রয়েছে গোল্ডেন রেসিও, গোল্ডেন স্পাইরালের স্পষ্ট উপস্থিতি। আর, হবে নাই বা কেন! দ্য ভিঞ্চির মধ্য বয়সের অঙ্কের শিক্ষক ছিলেন লুকা প্যাচিওলি (Luca Pacioli), যিনি গোল্ডেন স্পাইরাল নিয়ে রীতিমত অভিভূত হয়ে পড়েছিলেন! কাজেই তাঁর প্রভাব যে দ্যা ভিঞ্চির কাজের উপর পড়বে, তা বলাই বাহুল্য।

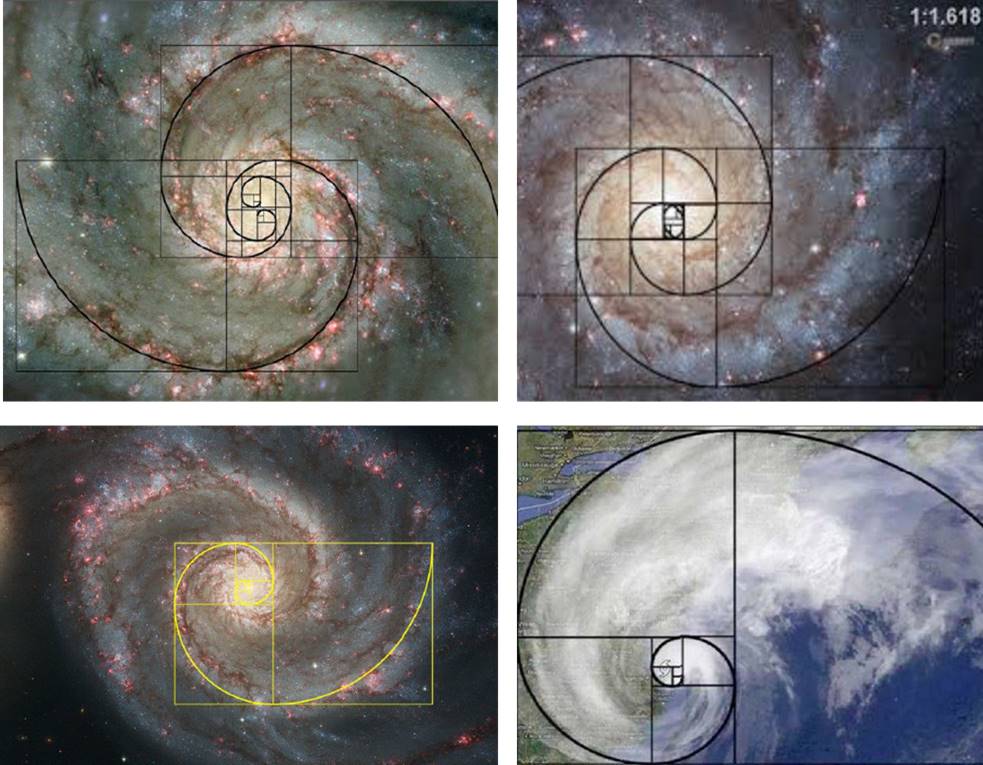
পেইন্টিং-এর মতো, ফটোগ্রাফিতেও গোল্ডেন রেসিও বা গোল্ডেন স্পাইরাল ব্যবহার করা হয় একটা ছবিকে দৃষ্টিনন্দন করে তোলার জন্য। চেষ্টা করা হয়, একটা ছবির ফ্রেম কে 1 : 1.618 এই অনুপাতে রাখতে। একটা সুন্দর ছবির ভিতর প্রথমেই চোখ যেখানে গিয়ে আটকে যায় (sweet spot), সেটা যদি একটা গোল্ডেন স্পাইরালের কেন্দ্র হয় তবে ছবির নান্দনিকতা যে অনেকাংশে বেড়ে যায় এটা পরীক্ষা করে দেখা গেছে।

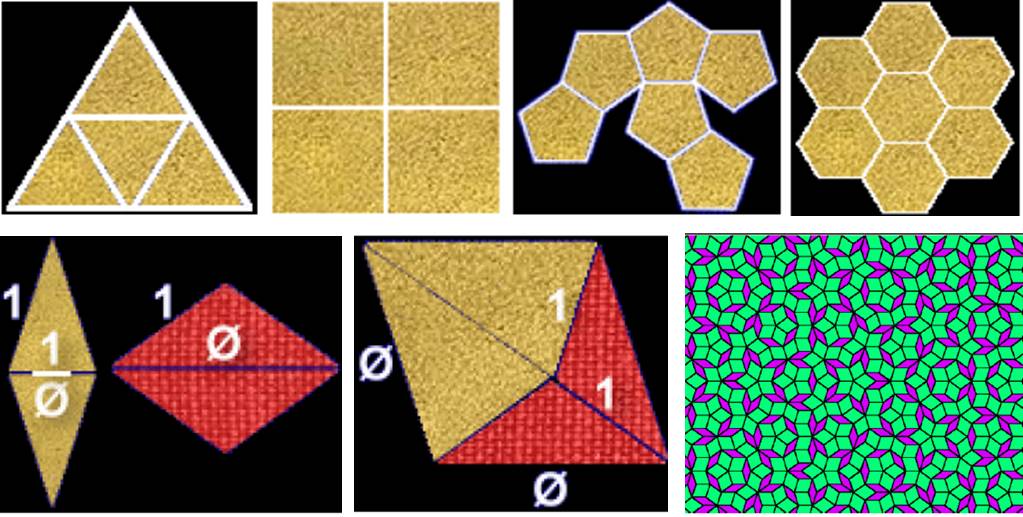
গ্রীকরা অবশ্য এই গোল্ডেন রেসিওর কথা অন্যভাবে জানতো, আর অবশ্যই জানতেন স্বয়ং ইউক্লিডও। তাই গ্রীক স্থাপত্য বিশ্লেষণ করে দেখা গেছে সেখানে গোল্ডেন রেসিওর উজ্জ্বল উপস্থিতি। গ্রীকদের শুভ চিহ্ণ সুষম পঞ্চভূজের মধ্যে কোণগুলো যোগ করে নানারকম লাইন টেনে দেখা গেছে তার মধ্যে এই গোল্ডেন রেসিও পাওয়া যাচ্ছে বিভিন্ন ভাবে। জ্যামিতিতে পারদর্শী গ্রীকরা যে এটা লক্ষ্য করবে এ তো স্বাভাবিক।

এখানেই শেষ নয়। পদার্থবিদ্যার অনেক গুরুত্বপূর্ণ ফর্মূলাতেও কিভাবে বেশ এসে যাচ্ছে এই গোল্ডেন রেসিও নাম্বার (গ্রীক লেটার ‘ফাই’ দিয়ে লেখা হয় একে)। নোবেল জয়ী পদার্থবিদ রজার পেনরোজ (Roger Penrose)-এর এক কালজয়ী কল্পনা ছিলো কোয়াসি-কেলাস-এর নক্সা (quasi crystal, অর্থাৎ ঠিক রেগুলার কেলাসের মত নয়, তার কাছাকাছি)। কখনো ভাবা যায় নি এরকমটা বাস্তবে সম্ভব হতে পারে। পেনরোজ দু’ধরণের জ্যামিতিক ইউনিট তৈরি করলেন (Kite এবং Dart এরকম দুটো জ্যামিতিক চিত্র) গোল্ডেন রেসিও (ফাই)-এর সাহায্যে। এগুলো দিয়ে তিনি একটা দ্বিমাত্রিক তলকে সম্পূর্ণ ভরাট করে দেখালেন (টেকনিক্যাল ভাষায় বলে tessellation) কিভাবে পঞ্চভূজের প্রতিসাম্য (five fold symmetry) তৈরি করা যায়, যা আগে কখনো ভাবা যায় নি। এইরকম একটা দ্বিমাত্রিক জ্যামিতি থেকে ত্রিমাত্রিক কোয়াসি কেলাসে রূপান্তর করে দেখা গেল, বাস্তবে তার উদাহরণ পাওয়া যাচ্ছে (কঠিন পদার্থের নতুন এই রূপ, এই কেলাসের জ্যামিতি কে ‘পেনরোজ ক্রিস্টাল’ বলে এখন। পরীক্ষাগারে এর প্রমাণ দিয়ে ২০১১ সালে রসায়নে নোবেল পান ইজরায়েলের ড্যানিয়েল স্কেটম্যান।)। আশ্চর্য ব্যাপার হলো, স্পেন এবং ইরানের অসাধারণ কিছু প্রাচীন মুসলিম স্থাপত্যের মধ্যে রয়েছে এই ধরণের জ্যামিতির উপস্থিতি। হয়ত অধ্যাপক পেনরোজ এসব দেখেই অনুপ্রাণিত হয়েছিলেন!

অঙ্ক তৈরির ভিত্তি হলো গণনা। গণনা করতে গিয়েই পরে তৈরি হয়েছে নানান রকম নাম্বার সিস্টেম। ইতিহাস তৈরিরও অনেক আগে, ৩৫ হাজার খ্রীষ্টপূর্বাব্দে আফ্রিকার সোয়াজিল্যান্ডে পাওয়া গিয়েছিলো বেবুনের হাড়ের ফসিল (Lebombo bone, সোয়াজিল্যান্ডের লেবোম্বো পাহাড়ে পাওয়া)। তাতে ধারালো পাথর দিয়ে নির্দিষ্ট গ্যাপে পর পর কিছু দাগ কাটা ছিল। এর পরে এরকম হাড়ের ফসিল আরো পাওয়া গেছে ফ্রান্সে এবং আফ্রিকার আরো কিছু জায়গায়। সবই মোটামুটি ৩৫ থেকে ২০ হাজার খ্রীষ্টপূর্ব সময়ের মধ্যেকার। নৃতত্ত্ববিদ্যা (Anthropology)-এর গবেষকরা বিশ্লেষণ করে দেখিয়েছেন, এইসব দাগ কেটে আসলে হিসাব রাখা হতো জীবনের কিছু পর্যায়বৃত্ত ঘটনা, আকাশের দিকে তাকিয়ে দেখা চাঁদের কলার নিয়মিত পরিবর্তন ইত্যাদির। আর, সেই থেকেই দাগ কেটে কেটে ট্যালি মার্কস দিয়ে গণনা করা আজো চালু আছে। রোমান সংখ্যার যে ডিজিট গুলো আমরা দেখি সেগুলো যে এরকম ট্যালি মার্কস বা আদিম যুগের দাগ কাটা থেকেই এসেছে তা বেশ বোঝা যায়। মানুষের সভ্যতার দীর্ঘ ইতিহাসে অনেক ভাবেই চেষ্টা হয়েছে নানারকম নাম্বার সিস্টেম তৈরি করার। মূলতঃ দৈনন্দিন হিসাব নিকাশ রাখার, ব্যবসা বা ট্যাক্সের কাজের সুবিধার জন্যই তা শুরু হয়েছিলো। এখন আমরা যে ইন্দো-আরবীয় দশমিক পদ্ধতি বা ডেসিমাল সিস্টেমে (base = 10) দশটা ডিজিট ব্যবহার করি তা স্বাভাবিক ভাবেই এসেছে দুহাতের দশটা আঙুল-এর গণনা থেকে। আসলে, ‘ডিজিট’ শব্দ এসেছে ল্যাটিন ‘ডিজিটাস’, মানে আঙুল থেকে।

পিসার লিওনার্দো-এর অঙ্কের বই, লিবার আবাচি কার্যত ইন্দো-আরব এবং ইউরোপ এই দুই দুনিয়ার মধ্যে অসাধারণ এক মেলবন্ধন ঘটিয়েছিল। এ যেন এক নিঃশব্দ বিপ্লব! মূলতঃ ব্যবসা-বাণিজ্যের কাজের সুবিধার জন্য লেখা হলেও ইউরোপের সাধারণ মানুষ জানলো ইন্দো-আরবীয় দশমিক পদ্ধতি, বীজগণিতের নিয়ম কানুন আর সেসবের গুরুত্ব। ইতিহাস পড়ে বোঝা যায়, ইন্দো-আরবীয় পদ্ধতিতে অঙ্ক করার পর থেকেই ইউরোপে অঙ্ক বিজ্ঞান, প্রযুক্তি আর অর্থনীতির অভাবনীয় অগ্রগতি হতে থাকে যা সারা পৃথিবীকে পরে সমৃদ্ধ করেছে। অথচ দুই দুনিয়ার এই সংযোগ স্থাপনের কারিগর পিসার লিওনার্দো থেকে গিয়েছেন বিস্মৃতির অন্তরালেই। পিসার মানুষেরাই প্রায় ভুলে গিয়েছিলো লিওনার্দোর কথা।

তবে, সুদীর্ঘ সময় পেরিয়ে, ১৬-শ শতকে লিওনার্দো পিসানো তথা ফিবোনাচি কে মনে রেখে তাঁর সুন্দর মার্বেলের একটা মুর্তি আর ফলক বসানো হয়েছিলো পিসা শহরের একটা স্কোয়ারে (Camposanto Monumentale in Miracle Square)। কখনো যদি পিসা বেড়াতে যাও, সেখানে অত্যাশ্চর্য হেলানো টাওয়ার দেখার সাথে লিওনার্দো পিসানোকেও দেখে আসতে পারো একবার।

[এই লেখার অনেক তথ্য নেওয়া হয়েছে Keith Devlin-এর লেখা বই, The Man of Numbers থেকে। এছাড়া উইকিপিডিয়া, ইউটিউব বা গুগুল সার্চ করলেই পাওয়া যাবে আরো অনেক তথ্য ও ছবি, জানা যাবে এ সংক্রান্ত আরো অনেক কিছু।]